1、然而，在这个问题中，#391e#39 是一个科学计数法的表示方式，它表示的是1乘以10的某个次方具体来说，#391e#39 就是1乘以10的0次方，也就是1科学计数法是一种表示大数或小数的方式，它通过将数字；数学上的e1也就是等于e啊不论是e的一次方，还是e乘以1，结果都是一样的，都是等于e数学上的e表示的是自然常数自然常数也是数学中一个常数，自然常数e是一个无限不循环小数，它的大小约为2值得一提的是，e不仅是数学常数，同时它也是自然对数函数的底数有时候也称e为欧拉数；次方是指将一个数连乘多次，例如2的4次方就是2×2×2×2 = 16e的正无穷次方是无穷大，而e的负无穷次方趋近于0对e的x次方求导数，当x大于1时，导数大于1，因此e的x次方在1到正无穷的区间内是单调递增的e，这个自然常数，是一个超越数，其值约为2它是自然对数函数的底数；作为数学领域的一个重要常数，它不仅是自然对数函数的底数，更被赋予了欧拉数以瑞士数学家欧拉命名和纳皮尔常数以纪念苏格兰数学家纳皮尔，他首先引入了对数概念的称谓这一数字，就像虚数单位i一样，成为了数学中不可或缺的一部分在所有数学常数中，e的知名度极高，堪称数学界的重要明星它；作为数学王国中的一位重要成员，它不仅是自然对数函数的底数，还拥有着多个不同的名字和来历首先，它常被称作欧拉数，以纪念瑞士数学家欧拉欧拉，这位18世纪的数学家，对微积分学和数学分析学做出了巨大的贡献，而自然常数e正是他研究；是一个无限不循环小数e的定义是自然对数的底数，也就是说，如果一个数的自然对数是1，那么这个数就是e同时，e也是微积分中的一个基础概念，它在求导数积分等运算中经常出现对于e的1次方，由于任何数的1次方都等于其本身，所以e的1次方；约等于272e一般指自然常数，是一个无限不循环小数，且为超越数，是自然对数函数的底数，其值约为2，四舍五入保留两位小数，也就是约等于272，而一次方指的是某个数的数值保持不变，任何数的一次方等于多少等于它本身，所以e的一次方等于它本身，也就是约等于272；当e的一次方被计算时，结果就是e本身，因为任何数的一次方就是它自己然而，e的零次方却是一个有趣的概念任何非零数的零次方都等于1，这是数学中的一个基本规则这个规则的背后是指数函数的性质，即任何数的零次方都相当于1这个规则的一。

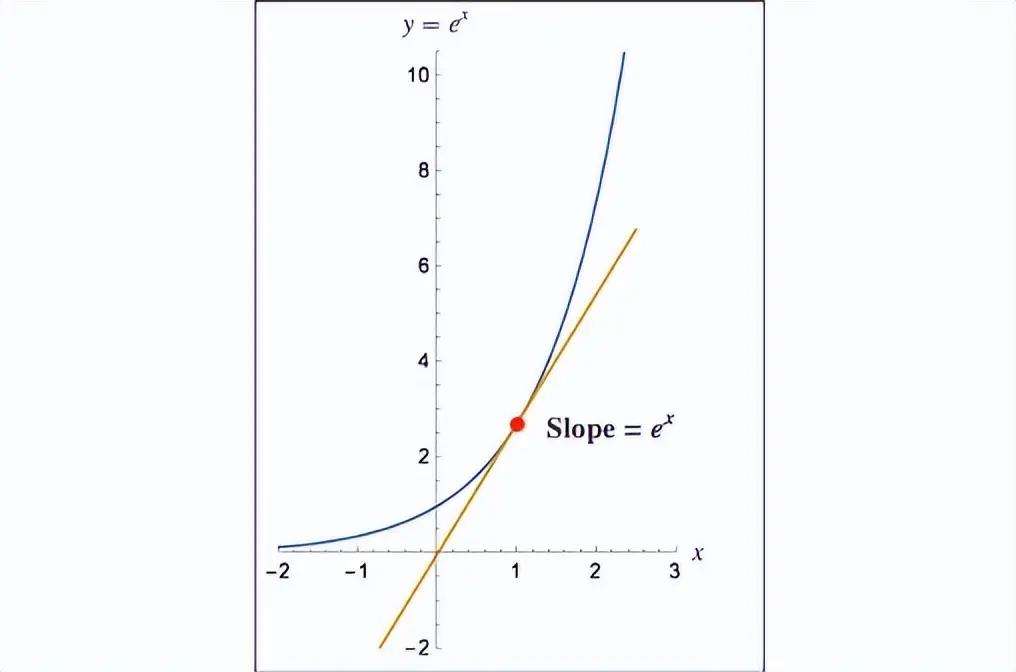
2、f0n阶导*x^n+拉格朗日余项这是一个误差项，计算中一般可忽略为是0e^x的导数还是e^x 所以e^1=e=e^0+1*e^0+12！*e^0*1^2+=1+1+12！+13！+14！++1n！e是1+1n^n的极限，当n趋于无穷时，这应该是e的来历，上面的式子是计算e的方法；对e的X次方求导数，当X大于1时，导数大于1所以当X趋向于无穷的时候导数必大于X=1时的导数1，挤大于1，因为导数大于零，所以在1到正无穷的区间内单调递增，所以为无穷e的本质 自然常数，符号e，为数学中一个常数，是一个无限不循环小数，且为超越数，其值约为2它是自然对数函数；它是自然对数函数的基础，也与欧拉和纳皮尔两位数学家的名字紧密相连就像圆周率π和虚数单位i一样，e在数学领域的地位举足轻重；e 的一次方等于e e = 2 e^1 = 2 一个数的一次方等于它本身详析次方最基本的定义是设a为某数，n为正整数，a的n次方表示为an，表示n个a连乘所得之结果，如2#8308=2×2×2×2=16次方的定义还可以扩展到0次方和负数次方等等在电脑上输入数学公式时；e的一次方就是e，代表的常数是e=2自然常数，符号e，为数学中一个常数，是一个无限不循环小数，且为超越数，其值约为2它是自然对数函数的底数次方最基本的定义是设a为任意数，n为正整数，a的n次方表示为a#8319，表示n个a连乘所得之结果，如2#8308=2×；e的0次方等于1，e的1次方等于e任何除0以外的数的0次方都是1，如3的0次方是1，有时称它为欧拉数Eulernumber，以瑞士数学家欧拉命名也有个较鲜见的名字纳。

3、该数字等于2根据一个数的一次方等于它本身，因为e等于2，e的1次方等于e，其中e是自然对数的底数，所以e的1次方等于2；为了更深入地理解这一点，我们可以考虑e的定义e是一个无限不循环小数，是连续复利增长中的一个重要常数它在数学物理和工程学中。

4、e的1次方等于e，以常数e为底数的对数叫做自然对数，记作lnNN0自然对数在物理学，生物学等自然科学中有重要的意义e是一个无限不循环小数，其值约等于2，它是一个超越数e作为数学常数，是自然对数函数的底数有时称它为欧拉数，以瑞士数学家欧拉命名也有个较鲜见的名字纳。