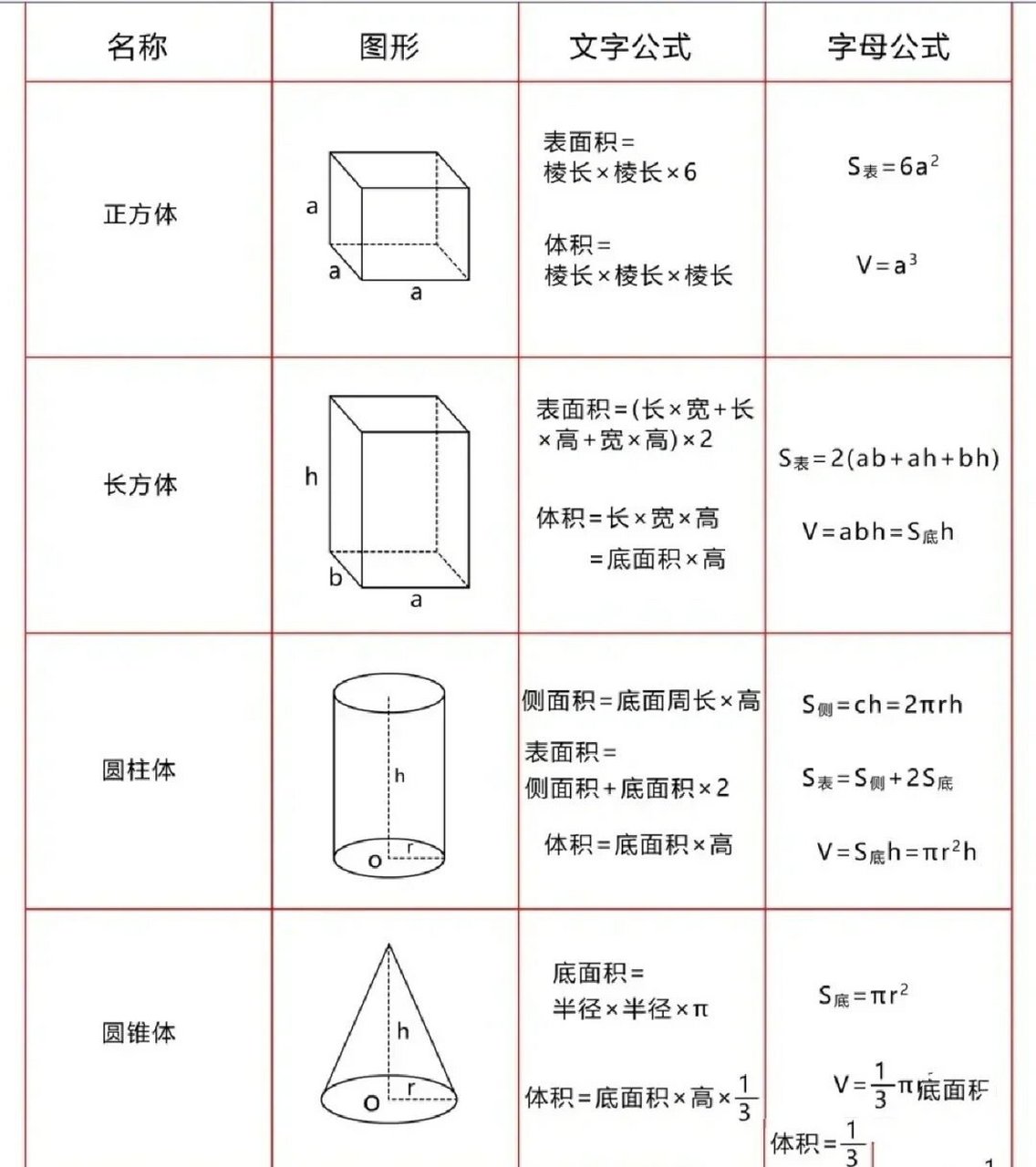
圆锥表面积的计算方法如下圆锥的表面积 = 底面积 + 侧面积 底面积圆锥的底是一个圆，其面积计算公式为 $S_底 = \pi r^2$，其中 $r$ 是圆锥底面的半径侧面积圆锥的侧面积展开后是一个扇形，其面积计算公式为 $S_侧 = \pi rl$，其中 $l$ 是圆锥的母线长，即从圆锥的；圆锥表面积公式S=πr#178+πrl圆锥表面积公式S=πr#178+πrl一个圆锥表面的面积叫做这个圆锥的表面积圆锥的表面积由侧面积和底面积两部分组成R是扇形半径，n是弧所对圆心角度数，π是圆周率，L是扇形对应的弧长也可以用扇形所在圆的面积除以360再乘以扇形圆心角的角度n，如下；简单分析一下，详情如图所示；在数学教育的阶梯上，人教版的六年级下册是学生们接触圆锥体表面积计算的重要阶段学生们会在这里系统地学习和掌握圆锥体表面积的计算方法这一概念虽然在小学阶段已经初露端倪，但在五年级或六年级的数学课程中，它通常出现在六年级下册学生们通过学习，能够理解圆锥体由底面和侧面构成，进而学习到如何；圆锥的表面积计算方法如下要知道圆锥的表面积是由哪两部分组成的圆锥的表面积是圆锥的侧面积和底面圆的面积的和哦先来计算圆锥的侧面积圆锥体的侧面积可以用圆周率π乘以圆锥体底面圆的半径r，再乘以圆锥的母线长l来计算公式是 πrl还有一个稍微复杂点的公式是母线长的平方乘以圆周率π。

S表=S底+S侧 其中S表为全面积，S底为底面积，S侧为侧面积锥体锥体是指包括圆锥棱锥等在内的空间立体图形，由圆的或其它封闭平面基底以及由此基底边界上各点连向一公共顶点的线段所形成的面所限定圆锥以直角三角形的一个直角边为轴旋转一周所得到的立体图形就是圆锥圆锥的计算公式S；圆锥的表面积计算方法如下要算底面积圆锥的底是一个圆，所以底面积就是圆的面积啦，公式是 π × r#178，其中 r 是圆锥的底面半径哦再算侧面积侧面积有点复杂，但是别担心，公式是 π × r × l，这里的 r 还是底面半径，l 是圆锥的母线长度，就是圆锥顶点到底面边缘那条线的；弧长等于圆锥体底面圆的周长的扇形和一个圆组成的，这个扇形又叫圆锥的侧面展开图圆锥的表面积=圆锥的侧面积+底面圆的面积 其中圆锥体的侧面积=πRL 圆锥体的全面积=πRl+πR2 π为圆周率314 R为圆锥体底面圆的半径 L为圆锥的母线长注意不是圆锥的高哦；以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的面所围成的物体叫做圆锥体圆锥由一个顶点，一个侧面和一个底面组成，从顶点到底面圆心的距离是圆锥的高圆锥有两个面，底面是圆形，侧面是曲面让圆锥沿母线展开，是一个扇形2计算圆锥底面积 圆锥的表面积公式中，πr#178。

圆锥体积V=13ShS是底面积，h是高圆锥表面积的计算公式是圆锥的表面积=底面积+侧面积侧面积将圆锥的侧面积不成曲线地展开，是一个扇形，用字母表示就是S=πr#178+πrl其中l=母线，是圆锥的顶点到圆锥的底面圆周之间的距离圆锥的表面积圆锥的表面积计算公式为S=π；圆锥体积公式v=13×s×h s是底面积=π×r×r h是高 ，π是圆周率即314 ，r是底圆半径 表面积公式S表=S底面积+S侧面积 圆锥的侧面积展开后是一个扇形，所以S侧面积=π×r×l r是底面半径 ，l是母线长；圆锥的表面积计算方法为圆锥的表面积 = 底面积 + 侧面积 底面积底面积是一个圆的面积，计算公式为 π × r^2，其中 r 是圆锥的底面半径侧面积侧面积的计算公式为 π × r × l，其中 l 是圆锥的母线长综合起来，圆锥的表面积计算公式可以表示为π × r × ，或者分开写为；表面积=底面积+侧面积底面积不用说，是πrsup2侧面积复杂一些因为圆锥侧面展开图是扇形，扇形的面积公式是12rl，这个r是扇形的半径，就是圆锥的母线长这个l是扇形的弧长，就是圆锥底面周长；圆锥的表面积计算公式为S圆锥表 = S侧 + S底 = πrL + πr#178，其中π为圆周率，r为底面半径，L为母线在计算圆锥表面积时，需要注意以下几点准确测量或给出底面半径r和母线L底面半径r是圆锥底面圆的半径，可以通过测量底面圆的直径后除以2得到母线L是圆锥顶点到底面圆上任意。

1圆锥的表面积计算表面积=底面积+侧面积r=半径，l=母线，π=圆周率即表面积=π·r2+？·2πr·l=π·r2+πrl=πr·l+r除了圆锥表面积的计算，圆锥的体积公式是三分之一底面积乘高，用字母表示为13πr2h2圆柱表面积=2πRR+h，圆柱体积=πR^2h，其中R表示圆柱的；圆锥体的表面积=πRL πR^2 R为圆锥体底面圆的半径 L为圆锥的母线长，不是圆锥的高 周长=2ΠR=ZΠX 圆锥的体积=13*πR^2h h圆锥体的高圆心角弧长*360周长 圆锥circular cone和棱锥pyramid这样的立体图形是锥体1以直角三角形的一个直角边为轴旋转一周所得到的立体图形就。