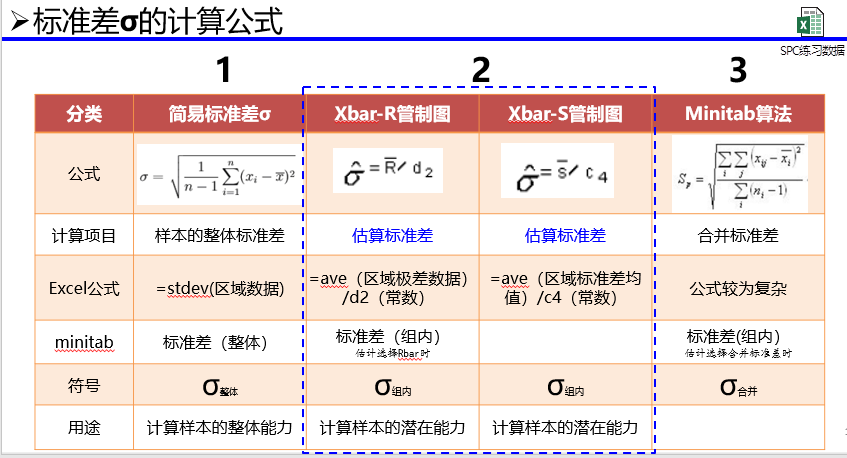
样本标准差公式有两种表示方式1样本标准差=方差的算术平方根=s=sqrtx1x2+x2x2+xnx2n1其中，xi表示各单个测量值，x表示所有测量值的均值，n表示所有测量值的总个数这个公式表示的是，每个测量值与均值的差的平方和，除以测量值的总个数减一，再取平方根。

样本标准差=方差的算术平方根=s=sqrt x1x^2 + x2x^2 + xnx^2n1 总体标准差=σ=sqrt x1x^2 + x2x^2 + xnx^2n什么是标准差由于方差是数据的平方，与检测值本身相差太大，人们难以直观的衡量，所以常用方差开根号换算回来这就。

1 样本标准差的计算公式为s = sqrtx1 x^2 + x2 x^2 + + xn x^2 n 12 样本标准差衡量的是样本数据点与样本平均值之间的离散程度它是方差的平方根，也被称为标准偏差或实验标准差3 标准差的公式是一个基本的数学公式，用于量化数据集。

样本标准差公式$s = sqrtfrac^2 + ^2 + ldots + ^2n1$其中，$barx$ 是样本均值，$x_1， x_2， ldots， x_n$ 是样本值，$n$ 是样本数量，$n1$ 是自由度总体标准差公式$sigma = sqrtfrac^2 + ^2 + ldots + ^2n$其中，$mu$ 是总体均值，$x。

标准差的计算公式如下样本标准差公式$s = sqrtfracsum_i=1^nx_i barx^2n1$解释其中，$s$ 表示样本标准差，$x_i$ 表示每个数据点，$barx$ 表示样本的平均值，$n$ 表示数据点的总数分母 $n1$ 是因为样本方差计算时采用无偏估计，需要减去1总体。

样本标准差公式为S = sqrt#178 解释如下样本标准差公式是描述一组数据离散程度的统计量它反映了样本中数据与样本均值之间的差异大小在公式中，S代表样本标准差，x代表每个观测值，x#772代表样本均值，n代表观测值的数量，Σ表示求和，sqrt表示开方运算具体来说，公式中的每一个。

$s^2 = frac1n1sum_i=1^nx_i barx^2$其中，$s^2$ 表示样本方差，$n$ 是样本数量，$x_i$ 是每一个样本值，$barx$ 是样本的平均值注意这里的分母是 $n1$，这是因为我们在计算样本方差时使用的是贝塞尔校正，以更好地估计总体方差样本标准差公式。

标准差计算公式如下样本标准差$s = sqrtfrac^2+^2+hellip+^2n1$，其中$n$是样本数量，$barx$是样本平均值，$x_1， x_2， hellip， x_n$是样本数据总体标准差$sigma = sqrtfrac^2+^2+hellip+^2n$，其中$n$是总体数量，$mu$是总体平均值，$x_1。

标准差计算公式分为总体标准差和样本标准差两种总体标准差公式为σ = sqrtx1x#773^2 + x2x#773^2 + hellip + xnx#773^2 n其中，σ 表示总体标准差，x1， x2， hellip， xn 是总体中的各个数值，x#773 是这些数值的平均值，n 是总体中的。

标准差的计算公式如下样本标准差公式为 $s = \sqrt\frac^2 + ^2 + \ldots + ^2n 1$其中，$x_1， x_2， \ldots， x_n$ 是样本数据，$\barx$ 是样本数据的平均值，$n$ 是样本数量分母使用 $n1$ 是因为样本方差的无偏估计需要这样调整总体标准差公式为。

2标准差公式意义 所有数个数为n记为一个数组n将数组的所有数求和后除以n得到算术平均值数组的所有数分别减去平均值，得到的n个差值分别取平方，再将得到的所有平方数求和，然后除以数的个数或个数减一若所求为总体标准差则除以n，若所求为样本标准差则除以n1，最后把得到的商取。

s=sqrtx1x^2+x2x^2+xnx^2n1样本标准差是总体各单位标准值与其平均数离差平方的算术平均数的平方根，即标准差是方差的平方根标准差公式是一种数学公式标准差也被称为标准偏差，或者实验标准差，公式样本标准差=方差的算术平方根=s=sqrtx1x。

标准差σ=方差开平方标准差是总体各单位标准值与其平均数离差平方的算术平均数的平方根即标准差是方差的平方根方差是离差的平方的加权平均数标准差怎么算 计算公式是什么 1标准差计算公式 标准差公式是一种数学公式标准差也被称为标准偏差，或者实验标准差，公式如下所示样本标准差=方差的。

标准差公式是一种数学公式标准差也被称为标准偏差，或者实验标准差，公式如下所示标准差计算公式标准差σ=方差开平方样本标准差=方差的算术平方根=s=sqrtx1x^2 +x2x^2 +xnx^2n1总体标准差=σ=sqrtx1x^2 +x2x^2 +xnx^2。